Given the agrarian origins of the one room schoolhouse, which gave Johnny summers off, to work in the fields, the curriculum was designed to be repetitive. Johnny would forget much of what he'd learned over the summer. Some review would be in order, come fall.
Around 8th or 9th grade, come Algebra, Johnny and Jill would learn about "functions", math objects one calls with arguments, getting something back. Or maybe they just pair inputs with outputs. During the New Math era, formal definitions were provided. Functions need not be numeric.
Along with functions, comes their composition. Given functions f and g, Johnny learns to write f(g(x)) and g(f(x)), but it all seems a tad meaningless and questions may be raised, by this or that student, regarding when these concepts will actually be used.
In the meantime, everything that happens on an industrial scale, tends to happen because of software, because of code. In learning to code, we learn about functions too, and their composition. One pipes to the next. Functions are chained together.
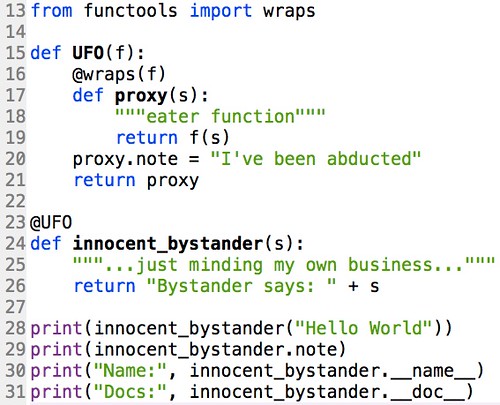
In the Python computer language, decorators are all about composition of functions. In the code below, from tonight's code school class, UFO "abducts" (composes with) innocent_bystander to return a well-disguised proxy, identical with the original right down to its docstring.
I use the ABC TV show Invasion as a stage-setter, for story, with no requirement that students watch it. The plot is clear enough: extraterrestrials in the lake eat and replace innocent humans with identical clones, so outwardly the same, that even the clones themselves do not suspect they're but proxies of their original selves.
CODE:
OUTPUT:
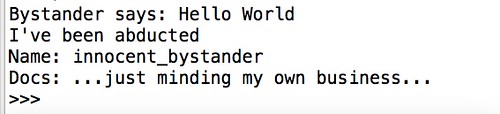
The @wraps decorator completes the disguise, carrying the __doc__ and __name__ attributes from the original to the proxy function. The cloning operation is complete.
Now that high schools are under some pressure to include coding, the question is: in what sort of course? The common assumption seems to be that any programming homework would logically fall under computer science, not mathematics, which is immune from needing computers, because well equipped with calculators.
Math students calculate. Computer science students compute. That difference is enough to drive a wedge through a school and unnecessarily multiply the number of times the same content is covered. In math, Johnny learns to calculate with vectors. In computer science, he learns to compute with them.
So on the one hand, we have mathematics looking for ways to prove relevance, and on the other, a discipline of proven relevance that's kept distinct from math, despite hitting a lot of the same topics.
Both math and computer science involve functions, plotting, algorithms, data structures, tabulation, summation.
However the assumption is math teachers cannot be retrained in place to add coding, because that's not what the textbooks include.
Innovation, original curriculum-writing, as a part of the math teacher's job description, seems too much of a stretch, despite teachers wishing to actually teach, and thereby regain higher status.
So not only is Jill given summers to forget, with repetitious fall reviews, but she's subjected to two separate approaches to a lot of the same material. Composition of functions is taught in math class, without much context, whereas computer science involves passing functions to functions that return functions. But we won't call that math.
Computer languages have the ability to take the drudgery out of repetitive computations, freeing the programmer to focus on the logic, the algorithms.
Rotating a polyhedron by applying the same rotation matrix to all its radial corner vectors, is tedious by hand, whereas once coded, happens at thirty frames a second or more.
Are polyhedrons and their scaling, rotations, translations, part of math or computer science? Will students learn about polyhedrons from two sets of textbooks?
Not only are Johnny and Jill subjected to yearly repetition and review, but the very same topics get covered within two different treatments.
Given all the unnecessary redundancy and repetition in the curriculum, accelerator programs have many ways to provide a head start and speed things up.
If we don't assume students are forgetting and starting over every year, plus learning the same concepts twice through two different treatments, we may be in position to at least double the curriculum's effectiveness.
What will serve Jill and Johnny well over the years are keyboarding classes. Coding is here to stay, at least for a good while, and it's primarily a keyboard activity, not a drag and drop graphical activity, Scratch notwithstanding. Typing remains an important skill across the board.
Around 8th or 9th grade, come Algebra, Johnny and Jill would learn about "functions", math objects one calls with arguments, getting something back. Or maybe they just pair inputs with outputs. During the New Math era, formal definitions were provided. Functions need not be numeric.
Along with functions, comes their composition. Given functions f and g, Johnny learns to write f(g(x)) and g(f(x)), but it all seems a tad meaningless and questions may be raised, by this or that student, regarding when these concepts will actually be used.
In the meantime, everything that happens on an industrial scale, tends to happen because of software, because of code. In learning to code, we learn about functions too, and their composition. One pipes to the next. Functions are chained together.
In the Python computer language, decorators are all about composition of functions. In the code below, from tonight's code school class, UFO "abducts" (composes with) innocent_bystander to return a well-disguised proxy, identical with the original right down to its docstring.
I use the ABC TV show Invasion as a stage-setter, for story, with no requirement that students watch it. The plot is clear enough: extraterrestrials in the lake eat and replace innocent humans with identical clones, so outwardly the same, that even the clones themselves do not suspect they're but proxies of their original selves.
CODE:
OUTPUT:
The @wraps decorator completes the disguise, carrying the __doc__ and __name__ attributes from the original to the proxy function. The cloning operation is complete.
Now that high schools are under some pressure to include coding, the question is: in what sort of course? The common assumption seems to be that any programming homework would logically fall under computer science, not mathematics, which is immune from needing computers, because well equipped with calculators.
Math students calculate. Computer science students compute. That difference is enough to drive a wedge through a school and unnecessarily multiply the number of times the same content is covered. In math, Johnny learns to calculate with vectors. In computer science, he learns to compute with them.
So on the one hand, we have mathematics looking for ways to prove relevance, and on the other, a discipline of proven relevance that's kept distinct from math, despite hitting a lot of the same topics.
Both math and computer science involve functions, plotting, algorithms, data structures, tabulation, summation.
However the assumption is math teachers cannot be retrained in place to add coding, because that's not what the textbooks include.
Innovation, original curriculum-writing, as a part of the math teacher's job description, seems too much of a stretch, despite teachers wishing to actually teach, and thereby regain higher status.
So not only is Jill given summers to forget, with repetitious fall reviews, but she's subjected to two separate approaches to a lot of the same material. Composition of functions is taught in math class, without much context, whereas computer science involves passing functions to functions that return functions. But we won't call that math.
Computer languages have the ability to take the drudgery out of repetitive computations, freeing the programmer to focus on the logic, the algorithms.
Rotating a polyhedron by applying the same rotation matrix to all its radial corner vectors, is tedious by hand, whereas once coded, happens at thirty frames a second or more.
Are polyhedrons and their scaling, rotations, translations, part of math or computer science? Will students learn about polyhedrons from two sets of textbooks?
Not only are Johnny and Jill subjected to yearly repetition and review, but the very same topics get covered within two different treatments.
Given all the unnecessary redundancy and repetition in the curriculum, accelerator programs have many ways to provide a head start and speed things up.
If we don't assume students are forgetting and starting over every year, plus learning the same concepts twice through two different treatments, we may be in position to at least double the curriculum's effectiveness.
What will serve Jill and Johnny well over the years are keyboarding classes. Coding is here to stay, at least for a good while, and it's primarily a keyboard activity, not a drag and drop graphical activity, Scratch notwithstanding. Typing remains an important skill across the board.