Copied from Facebook:
The way I sometimes teach it is we go over A x B the usual way, with A and B perpendicular, and then of course we don't just draw a line from A-tip to B-tip (common origin), we double that triangle to make a full rectangle, filled with squares. That's our civilizational orthodoxy.
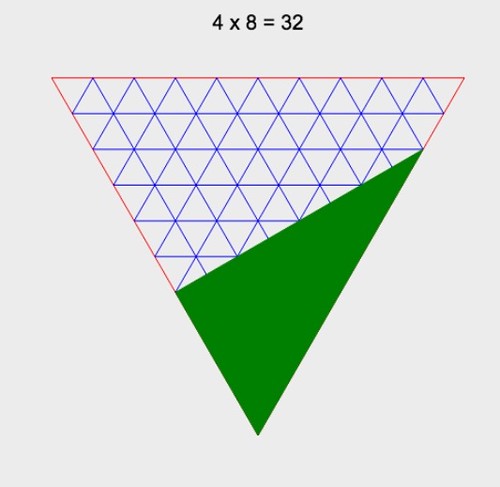
Imagine not doing that final doubling and defining A x B as simply "closing the lid" on that right triangle. A x B is always a right triangle (the same area might be any shape, but that's the canonical representation).
Next, we take the extra step of making the angle 60 degrees instead of 90 (yes, it's somewhat arbitrary but 60 has attractive features our ETs may have felt drawn to). We simply draw A and B as vectors at 60 degrees with a common origin, and define A x B as "closing the lid". This is what you see above.
What I'm not showing here is the next step, adding C, another vector, such that A x B x C is three arrows from the corner of a regular tetrahedron. Again, we simply "close the lid" such that volume A x B x C is the tetrahedron with "lid" ABC (origin O).
We spend some time dwelling on the logical consistency of this logical beginning, before coming back full circle to our Earthian cube. A,B, C must be mutually perpendicular and the right tetrahedron formed by "closing the lid" is only 1/6th of the full hexahedron's volume -- a different approach. Earthians are very right-angle minded.
How will these civilizations get along? Stay tuned. The ETs have a unit volume tetrahedron (1 x 1 x 1 = 1) and use that to anchor volumes of other polyhedrons. A cube, with thrice the volume, when edges = face diagonals, has volume 3 (consistently). Octahedron has volume 4 (same edge lengths). Nice whole numbers. Earthians agree on the ratios, just don't share the same model of 3rd powering (hexahedral versus tetrahedral).
ET means "extraterrestrial" i.e. I'm couching this analysis (aka lesson plan) in the science fiction form. An "outer space" civilization has a different way of modeling 3rd powering based on the regular tetrahedron instead of a cube. We appreciate the logic of their civilization, but don't abandon our own. That's like the TV Guide version. A goal of this lesson is to help students get philosophical and think about foundational questions i.e. what's conventional and what are examples of different flavors of math, thanks to different conventions.
The way I sometimes teach it is we go over A x B the usual way, with A and B perpendicular, and then of course we don't just draw a line from A-tip to B-tip (common origin), we double that triangle to make a full rectangle, filled with squares. That's our civilizational orthodoxy.
Imagine not doing that final doubling and defining A x B as simply "closing the lid" on that right triangle. A x B is always a right triangle (the same area might be any shape, but that's the canonical representation).
Next, we take the extra step of making the angle 60 degrees instead of 90 (yes, it's somewhat arbitrary but 60 has attractive features our ETs may have felt drawn to). We simply draw A and B as vectors at 60 degrees with a common origin, and define A x B as "closing the lid". This is what you see above.
What I'm not showing here is the next step, adding C, another vector, such that A x B x C is three arrows from the corner of a regular tetrahedron. Again, we simply "close the lid" such that volume A x B x C is the tetrahedron with "lid" ABC (origin O).
We spend some time dwelling on the logical consistency of this logical beginning, before coming back full circle to our Earthian cube. A,B, C must be mutually perpendicular and the right tetrahedron formed by "closing the lid" is only 1/6th of the full hexahedron's volume -- a different approach. Earthians are very right-angle minded.
How will these civilizations get along? Stay tuned. The ETs have a unit volume tetrahedron (1 x 1 x 1 = 1) and use that to anchor volumes of other polyhedrons. A cube, with thrice the volume, when edges = face diagonals, has volume 3 (consistently). Octahedron has volume 4 (same edge lengths). Nice whole numbers. Earthians agree on the ratios, just don't share the same model of 3rd powering (hexahedral versus tetrahedral).
ET means "extraterrestrial" i.e. I'm couching this analysis (aka lesson plan) in the science fiction form. An "outer space" civilization has a different way of modeling 3rd powering based on the regular tetrahedron instead of a cube. We appreciate the logic of their civilization, but don't abandon our own. That's like the TV Guide version. A goal of this lesson is to help students get philosophical and think about foundational questions i.e. what's conventional and what are examples of different flavors of math, thanks to different conventions.